Multiresolution Blending and Hybrid Images

Written on September 27th, 2018 by Andrew Campbell

This post explores a few applications of image processing in the frequency domain, including image sharpening and the synthesis of hybrid images. We also use Gaussian and Laplacian stacks to perform multiresolution blending, which is the process of computing a gentle seam between two images at each band of image frequencies.

Note: This was originally done as part of a project for CS194-26, a course on computational photography at UC Berkeley.

Introduction to Frequencies: Sharpening

Background

Frequency means the rate of change of intensity per pixel. The fewer the pixels it takes to represent that intensity variation, the higher the frequency. Generally speaking, any feature that can be described as an “edge” or “border”, is a high frequency feature because it’s characterized by a relatively sharp transition in the intensity profile.

It is closely connected to the concept of an image gradient, which is the directional change in the intensity or color in an image. Smooth gradients represent low frequencies and sharp gradients represent high frequencies.

Unsharp Masking Filter

The unsharp masking filter, contrary to it’s name, is a common algorithm for sharpening an image. It works by utilizing a slightly blurred version of the original image which is then subtracted away from the original to detect the presence of edges, creating the unsharp mask (effectively a high-pass filter). By adding the mask back to the original image, contrast is selectively increased along the edges, leaving behind a sharper final image.

$\text{im}_{\text{sharp}} = \text{im}_\text{og} + \alpha(\text{im}_\text{og} - \text{im}_\text{blur})$

A simple Gaussian blur suffices for the blurred image; I used a $ 9 \times 9 $ Gaussian kernel with $ \sigma = 10 $. Using $ \alpha = 0.5 $, here are some of the before-and-after results:

Hybrid Images

Background

Hybrid images are static images that change in interpretation as a function of the viewing distance. The basic idea is that high frequency tends to dominate perception when it is available, but, at a distance, only the low frequency (smooth) part of the signal can be seen. By blending the high frequency portion of one image with the low-frequency portion of another, you get a hybrid image that leads to different interpretations at different distances.

Implementation

We begin by finding pairs of images we want to turn into hybrid images and aligning on 2-point correspondences, e.g. eyes. To low-pass filter one image, we simply apply a Gaussian blur. To high-pass filter the other image, we subtract the Gaussian-filtered image from the original (this is the same idea as the unsharp filter discussed above).

The Gaussian kernel sizes used to create the low-pass and high-pass filter determine the low-frequency-cutoff and the high-frequency-cutoff, respectively. Through some experimentation I found that 35 worked well for the high-frequency-cutoff and 61 worked well for the low-frequency-cutoff. I again used $ \sigma = 10 $ for the kernels.

Lastly we simply add the two images. I kept color in both the low-pass and high-pass images and thought the result looked good. Here are some of the results; for maximum effect, look at the images from both close-up and far-away and see how your perception changes.

Not all pairings were quite so successful:

The images should ideally have similar features and be of similar color for the best effect.

Frequency analysis

Here we illustrate the process by showing the log magnitude of the Fourier transform of the two input images, the filtered images, and the hyrbid image, respectively.

Gaussian and Laplacian Stacks

An image pyramid is a multi-scale signal representation of an image in which an image is subject to repeated smoothing and subsampling. An stack is similar to a pyramid, but without the downsampling.

In a Gaussian stack, subsequent images are weighted down using a Gaussian blur. A Laplacian stack is constructed from a Gaussian stack: each layer stores the difference between the corresponding Gaussian layer and the level above it (the first level is the difference between the original image and first level Gaussian).

By visualizing the Gaussian and Laplacian stacks for images that contain structure in multiple resolutions, we can extract the structure at each level. Shown below are the Gaussian stacks (top) and Laplacian stacks (bottom) for some interesting images.

Notice the Mona Lisa’s smile does not appear until we filter out the high-frequencies.

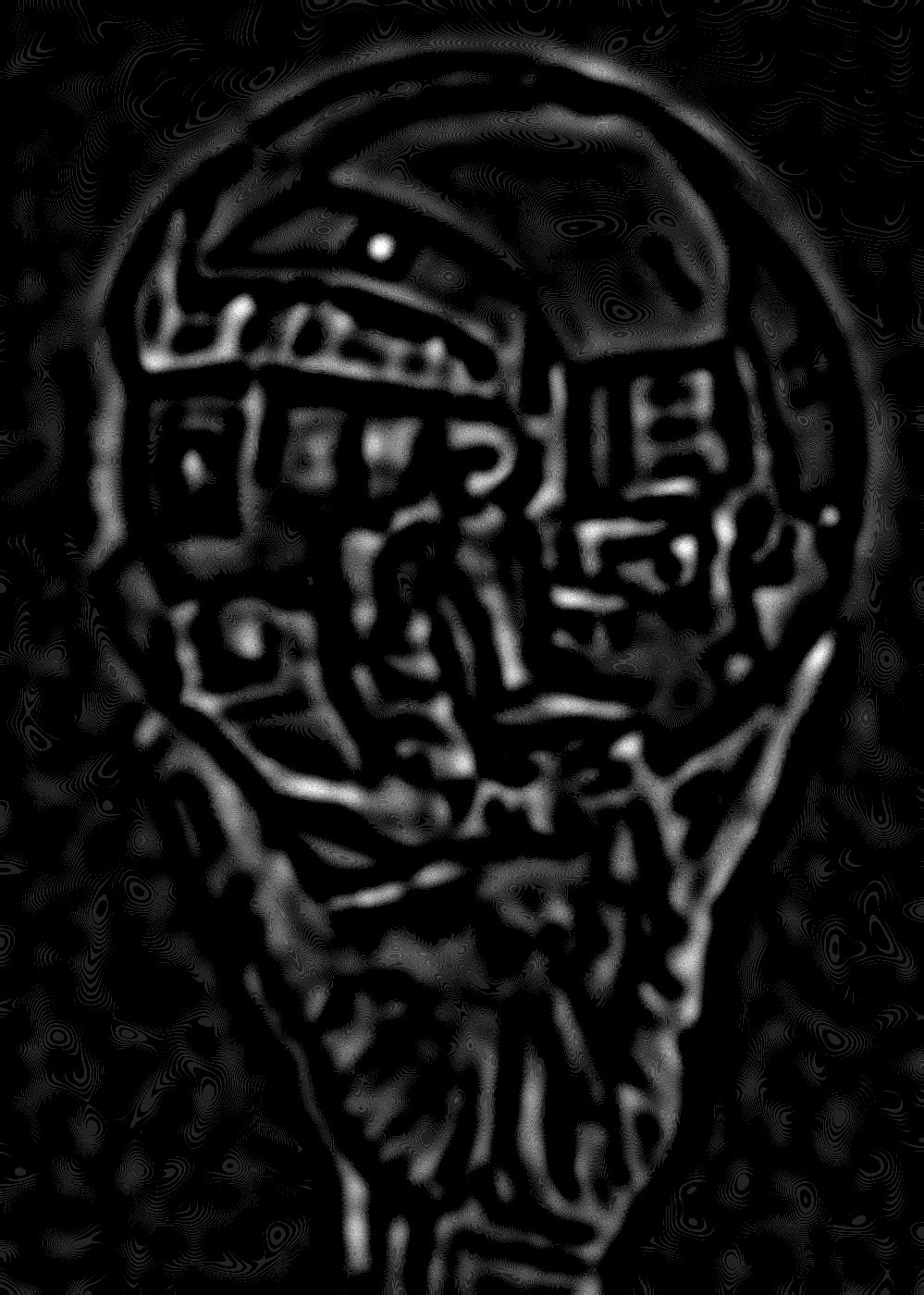
Different structures come to light at different levels in the stack for surrealist artist M. C. Escher’s Hand with Reflecting Sphere.

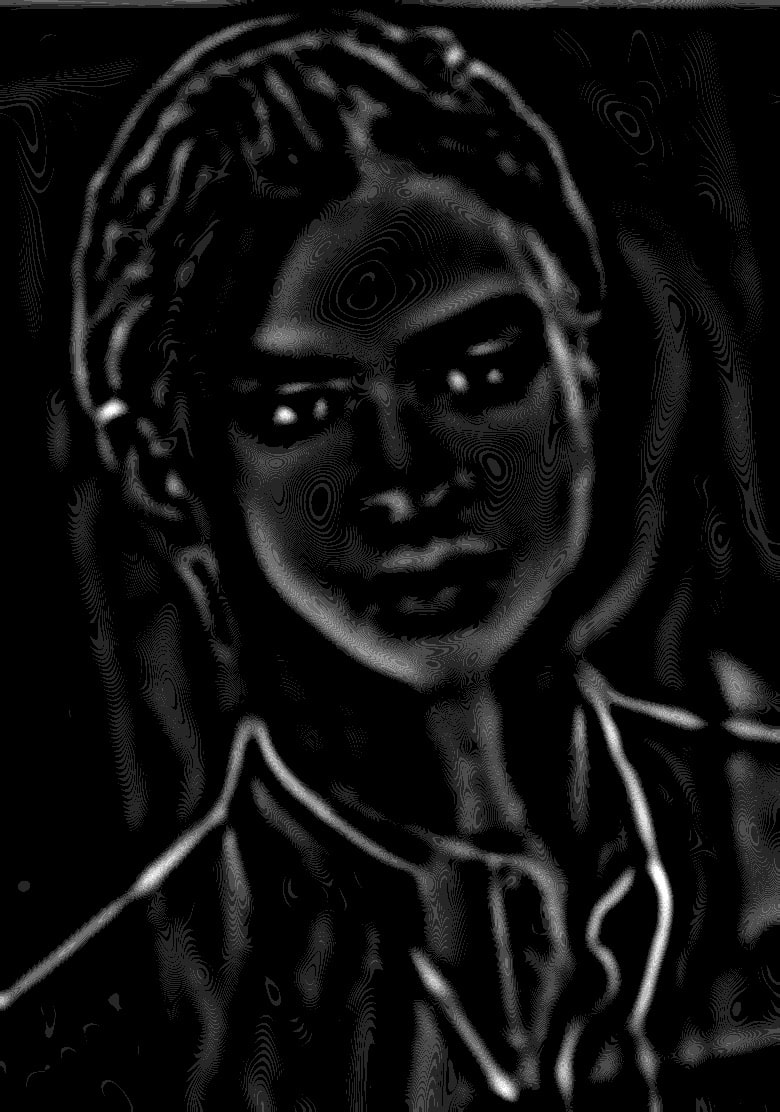
Looking at the stacks for the hybrid image we created earlier reveals the transition from high-frequency Ansel Elgort to low-frequency Lily Collins, as expected.

Multiresolution Blending

An image spline is a smooth seam joining two image together by gently distorting them. Multiresolution blending computes a gentle seam between the two images seperately at each band of image frequencies, resulting in a much smoother seam.

We use a slight modification of the algorithm presented in the 1983 paper by Burt and Adelson. At a high-level, the steps are as follows:

For input images A and B (of the same size), build Laplacian stacks $ LA $ and $ LA $.
Create a binary-valued mask M representing the desired blending region.
Build a Gaussian stack $ GM $ for M.
Form a combined stack $ LS $ from $ LA $ and $ LB $ using values of $ GM $ as weights. That is, for each level $ \ell $, $LS_{\ell}[i,j] = GM_{\ell}[i,j] LA_{\ell}[i,j] + (1 - GM_{\ell}[i,j]) LB_{\ell}[i,j].$
Obtain the splined image S by expanding and summing the levels of $ LS $.

Essentially what we’re doing is using higher feathering on low-frequency parts of the image and lower feathering on high-frequency parts of the image.

Some results using vertical masks are shown below: